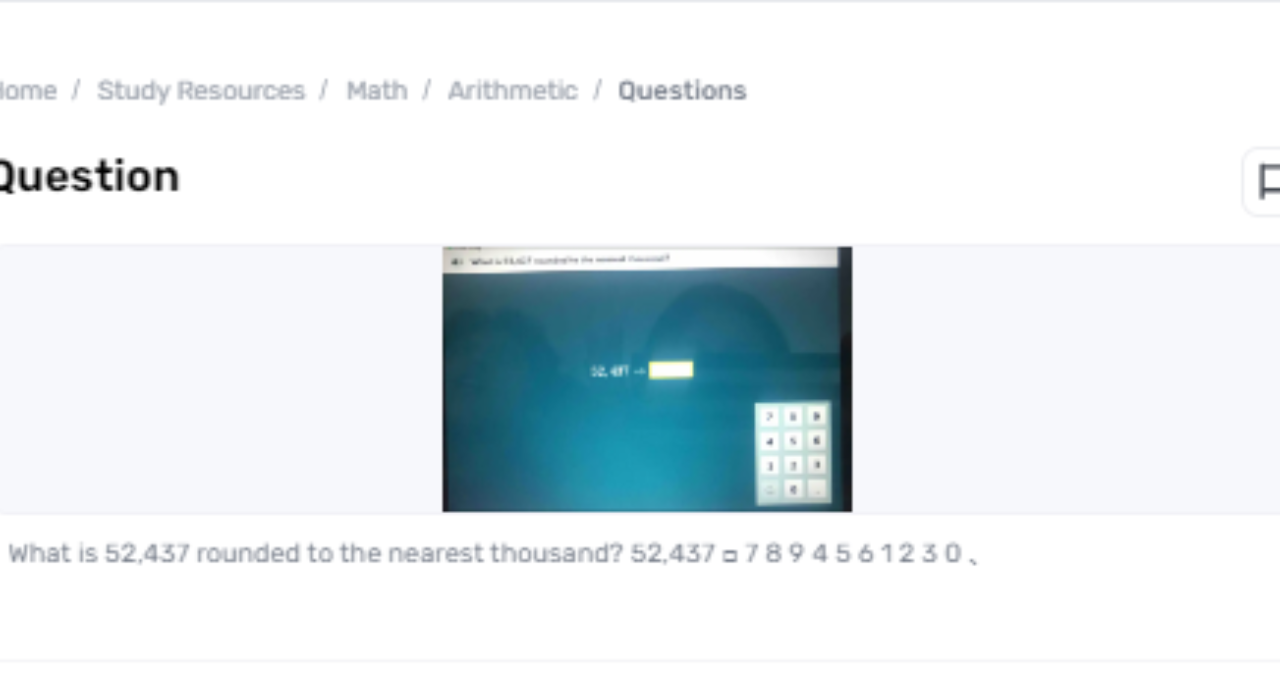
Adjusting numbers could be a principal numerical concept utilized to rearrange calculations and show information in a more sensible frame. When managing expansive numbers, adjusting to a particular set of esteem can make it simpler to get it and work with the numbers in various practical applications. In this exposition, we are going investigate the method of adjusting the number 52437 rounded to the nearest thousand. This case will illustrate how adjusting works and the steps included in achieving a rearranged surmised esteem.
Understanding the Adjusting Handle
Adjusting numbers involves approximating a number to make it less demanding to work with, based on an indicated put esteem. The fundamental guideline of adjusting is to decide which esteem a number is closest to inside the chosen place value. For occurrence, adjusting to the closest thousand implies finding the closest difference of 1,000 to the given number. This handle is guided by the digit within the put quickly right of the put esteem being adjusted to. In our illustration, we are adjusting 52,437 to the closest thousand, which needs analyzing the hundreds of digits to choose whether to circular up or down.
Distinguishing the Put Esteem
From circular 52,437 to the closest thousand, we begin with distinguishing the pertinent digits. The number 52,437 can be broken down as follows: Thousands Put 52,000, Hundreds Put: 437
The closest thousand put is spoken to by the digit within the thousands put (2 in this case), and the hundreds put (4 in this case) will decide whether to round up or down. When adjusting, we see the digit quickly to the proper of the thousands put (which is within the hundreds put) to choose whether to circular up or down.
Adjusting Rules
The standard adjusting rules are clear:
If the digit within the put quickly right of the adjusting place (hundreds put in this case) is 5 or more prominent, circular up. If the digit is less than 5, circular down. In our case, the hundreds put the digit in 52,437 is 4. Since 4 is less than 5, we circular down concurring to the adjusting rules. This implies we don't increment the thousands place digit but maybe keep it because it is.
Applying the Adjusting Rules
Applying the adjusting rules to 52,437, we watch that the hundreds put digit (4) is less than 5. Subsequently, we circular down. To circular 52,437 to the nearest thousand: Keep the thousands put digit the same. This digit is 2, which speaks to 52,000. Supplant the digits to the correct of the thousands put with zeros. This comes about within the adjusted number of 52,000. In this way, 52,437 adjusted to the closest thousand is 52,000.
Viable Suggestions of Adjusting
Adjusting numbers is broadly utilized in different areas such as fund, information investigation, and way of life to rearrange and inexact values. For occasion, in budgetary explanations, adjusting to the closest thousand can make expensive figures more comprehensible and less demanding to communicate. In information investigation, rounding can help in summarizing information and making speedy gauges. Essentially, in day-by-day exercises like budgeting or assessing separations, adjusting makes a difference in making speedy choices without getting hindered by exact numbers.
Strategy for Reacting to a Gauth Inquiry
1. Identify the Issue:
Decide whether the question relates to setup, usage, management, or investigating to center your reaction.
2. Gather Important Information:
Audit Gauth’s official materials and common issues to guarantee you give a total and exact reply.
3. Formulate the Reaction:
Organize the data in a clear, step-by-step arrangement, ensuring it straightforwardly addresses the address.
4. Review and Refine:
Confirm the points of interest for accuracy and upgrade the reaction for clarity and conciseness, making it simple to get.
Conclusion
In conclusion, adjusting 52,437 to the closest thousand includes an efficient approach that streamlines the number based on its vicinity to the closest numerous of 1,000. By following the standard adjusting rules and analyzing the hundreds put digit, we decide that 52,437 adjusted to the closest thousand is 52,000. This process of adjusting makes huge numbers more sensible and maybe a profitable apparatus in different viable applications. Understanding how to circular numbers accurately is fundamental for compelling communication, calculation, and decision-making in numerous viewpoints of life.